Rational equations demand a unique approach, often involving worksheets for focused practice; readily available PDF resources offer solutions for self-assessment and skill enhancement.

Mastering these techniques is crucial for success in algebra and related mathematical fields, building a strong foundation for future concepts.

These worksheets, like those by Kuta Software, provide structured exercises and solutions, aiding comprehension and problem-solving abilities.

Tyler Wallace’s resources, under a Creative Commons license, further support learning, offering accessible materials for students and educators alike.

What are Rational Equations?

Rational equations are algebraic equations that contain one or more rational expressions – fractions where the numerator and denominator are both polynomials.

These equations are solved by finding values for the variable that make the equation true, much like standard algebraic equations, but with added considerations.

Worksheets focusing on solving rational equations, often available as PDF downloads, present these equations in various forms, requiring students to demonstrate proficiency in manipulating fractions and solving for unknowns.

Examples include equations like 9/5 = 4/(3x + 1) or 3x/4 ‒ 1/x = 2, commonly found in practice materials from sources like Kuta Software.

Successfully tackling these requires understanding how to clear denominators and check for extraneous solutions, a key skill emphasized in instructional resources.

These equations are fundamental in algebra and build a strong foundation for more complex mathematical concepts.

Why are they Important?

Rational equations aren’t merely abstract exercises; they model real-world scenarios involving rates, ratios, and proportions, making them crucial for applied problem-solving.

Understanding these equations is vital in fields like physics, engineering, and economics, where relationships are often expressed as fractional functions.

Solving rational equations worksheets, particularly those with provided answers PDF format, offer targeted practice, reinforcing the necessary skills for these applications.

Mastering these concepts builds a strong algebraic foundation, preparing students for more advanced coursework like calculus and differential equations.

Resources like those by Tyler Wallace and Kuta Software LLC emphasize the importance of checking for extraneous solutions, a critical step in ensuring accuracy.

Developing proficiency in this area enhances analytical thinking and problem-solving capabilities, valuable assets in any discipline.

Understanding Rational Expressions

Rational expressions form the basis of these equations; worksheets with answers PDF help students identify and manipulate these expressions effectively for problem-solving.

Defining Rational Expressions

Rational expressions are fundamentally fractions where both the numerator and denominator are polynomials. Understanding this core definition is paramount when tackling solving rational equations, and worksheets – particularly those available as PDF documents with included answers – provide excellent practice.

These worksheets, such as those created by Kuta Software LLC, often begin by reinforcing this basic concept before moving onto more complex equation solving. They emphasize recognizing polynomial structures within the fractions.

Successfully identifying these expressions is the first step towards manipulating them correctly. Resources like those from Tyler Wallace, licensed under Creative Commons, further clarify this foundational element, offering accessible explanations and examples. Mastering this definition unlocks the ability to find the Least Common Denominator (LCD), a crucial step in solving these equations.

Identifying Restrictions on the Variable

When working with rational equations, and specifically utilizing a solving rational equations worksheet with answers PDF, recognizing variable restrictions is critical. These restrictions arise because division by zero is undefined. Therefore, any value of the variable that makes the denominator of a rational expression equal to zero must be excluded from the solution set.

Worksheets, like those from Kuta Software, consistently emphasize this step, often requiring students to explicitly state these restrictions before solving. Failing to do so can lead to extraneous solutions.

Resources from Tyler Wallace reinforce this concept, highlighting its importance in maintaining the integrity of the mathematical process. Identifying these restrictions ensures that only valid solutions are accepted, preventing errors and fostering a deeper understanding of rational functions.

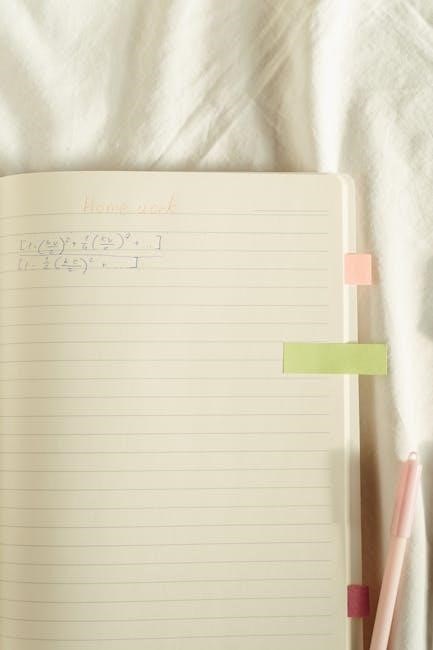
The Least Common Denominator (LCD)

Worksheets for solving rational equations, often in PDF format, prioritize finding the LCD to eliminate fractions, simplifying the equation for easier manipulation and solution.

Finding the LCD of Rational Expressions

Determining the Least Common Denominator (LCD) is foundational when tackling rational equations, and worksheets – frequently available as PDFs with solutions – heavily emphasize this skill. The LCD is constructed by identifying all unique factors present in the denominators of the rational expressions.

Each factor is then taken to the highest power it appears in any single denominator. For instance, if denominators include (x-2) and (x+1)², the LCD would be (x-2)(x+1)².

Many worksheets, like those from Kuta Software, provide practice problems specifically designed to build proficiency in finding the LCD. Mastering this step is crucial, as it prepares the equation for subsequent simplification and solving, ultimately leading to accurate results and a deeper understanding of the concepts.

Multiplying Both Sides by the LCD

Once the Least Common Denominator (LCD) is identified, the next critical step in solving rational equations – often practiced through worksheets in PDF format – involves multiplying both sides of the equation by the LCD. This strategic move effectively eliminates the fractions, transforming the rational equation into a more manageable polynomial equation.

Each term on both sides must be multiplied by the LCD, carefully distributing to ensure accuracy. This process leverages the distributive property to cancel out the denominators.

Worksheets, such as those offered by Kuta Software and resources from Tyler Wallace, provide ample opportunities to practice this technique, with included solutions for verification. This step is paramount for isolating the variable and progressing towards a solution.

Solving Rational Equations: Step-by-Step

Worksheets, often in PDF format, guide you through solving these equations: find the LCD, multiply both sides, simplify, and solve for the variable.

Step 1: Find the LCD

Identifying the Least Common Denominator (LCD) is the foundational first step when tackling rational equations, as highlighted in numerous solving rational equations worksheet examples.

This involves examining all denominators within the equation and determining the smallest polynomial expression that each denominator divides into evenly.

PDF worksheets frequently begin with exercises specifically designed to practice finding the LCD, building this crucial skill before progressing to full equation solving.

For instance, if denominators are ‘x’, ‘2x’, and ‘x+1’, the LCD would be ‘2x(x+1)’.

Kuta Software worksheets emphasize this initial step, providing ample practice opportunities.

Accurately determining the LCD is paramount, as it’s used to eliminate fractions, simplifying the equation and paving the way for a straightforward solution.

Remember to factor denominators completely to ensure you find the least common denominator.

Step 2: Multiply Both Sides by the LCD

Once the Least Common Denominator (LCD) is identified, the next crucial step involves multiplying every term on both sides of the rational equation by this LCD.

This action strategically eliminates the fractions, transforming the rational equation into a more manageable polynomial equation.

Solving rational equations worksheet materials, often available as PDF downloads, consistently demonstrate this technique.

Ensure each term, not just the fractions, is multiplied; distribution is key!

Worksheets by Kuta Software LLC and resources from Tyler Wallace explicitly guide students through this process.

This step is vital because it simplifies the equation, allowing for standard algebraic techniques to be applied to solve for the variable.

Careful distribution and simplification are essential to avoid errors at this stage.

Step 3: Simplify and Solve the Resulting Equation

After multiplying both sides by the LCD, the equation should be free of fractions. Now, meticulously simplify by combining like terms and expanding any remaining products.

This often leads to a standard polynomial equation – linear, quadratic, or higher order – solvable using familiar algebraic methods like factoring, the quadratic formula, or simple isolation of the variable.

Solving rational equations worksheet examples, particularly those in PDF format, showcase this simplification process.

Resources from Kuta Software LLC and Tyler Wallace provide step-by-step solutions.

Remember to maintain accuracy during simplification, as errors here propagate through the remaining steps.

Once simplified, apply appropriate techniques to isolate the variable and determine potential solutions.

Extraneous Solutions

Worksheets emphasize checking solutions, as multiplying by the LCD can introduce extraneous roots – values that satisfy the transformed equation, but not the original.

PDF resources detail this verification process.

What are Extraneous Solutions?

Extraneous solutions are values that appear to solve a rational equation after the solving process, but do not actually satisfy the original equation. They arise primarily when manipulating rational expressions, specifically when multiplying both sides of the equation by the least common denominator (LCD).

This multiplication can sometimes introduce solutions that make the original denominators zero, which is undefined in rational expressions. Worksheets focusing on solving rational equations, often available as PDF documents with answers, consistently stress the importance of checking each potential solution.

Kuta Software’s resources, for example, explicitly instruct students to “remember to check for extraneous solutions” after solving each equation. These extraneous roots are essentially false positives, and identifying them is a critical step in ensuring the accuracy of the solution set. Failing to check can lead to incorrect answers.

Checking for Extraneous Solutions

Checking for extraneous solutions is a vital final step when solving rational equations. It involves substituting each potential solution back into the original equation to verify its validity. If a value causes any denominator to equal zero, it’s an extraneous solution and must be discarded.

Worksheets, particularly those in PDF format with provided answers, emphasize this process. Resources like those from Kuta Software LLC explicitly state, “Solve each equation. Remember to check for extraneous solutions.” This reinforces the necessity of verification.

Elementary Algebra skill practice sheets also highlight this crucial step. By plugging the solution back into the original equation, you confirm whether it truly satisfies the equation’s conditions, avoiding incorrect results. This practice builds a robust understanding of rational equation solving.

Types of Rational Equations

Worksheets present both simple and complex rational equations; PDF resources offer varied practice, building skills to tackle diverse problems and solutions.

Simple Rational Equations

Simple rational equations, frequently found on solving rational equations worksheets, typically involve a single rational expression set equal to a constant or another simpler expression. These equations often require only basic algebraic manipulation to isolate the variable, such as multiplying both sides by the common denominator.

PDF worksheets, like those provided by Kuta Software LLC, often begin with these types to build confidence. These exercises focus on clearing fractions and solving linear equations, reinforcing fundamental skills. Remember to always check for extraneous solutions, even in seemingly straightforward cases, as highlighted in many practice materials.

These introductory problems serve as a stepping stone to more complex scenarios, ensuring a solid understanding of the core principles before tackling more challenging rational equations. The provided answer keys within the PDF allow for immediate self-assessment and error correction.

Complex Rational Equations

Complex rational equations, often featured in advanced sections of solving rational equations worksheets, present a greater challenge. These equations involve rational expressions within other rational expressions, demanding a more strategic approach to simplification. Techniques include finding a common denominator for the entire equation or simplifying the numerator and denominator separately before solving.

PDF resources, such as those from Kuta Software, dedicate sections to these intricate problems, providing step-by-step solutions as guidance. These worksheets emphasize careful algebraic manipulation and a thorough understanding of fraction operations. Don’t forget the crucial step of checking for extraneous solutions!

Mastering these equations requires practice and a solid grasp of foundational concepts. Utilizing the answer keys in the PDF allows for immediate feedback and reinforces correct problem-solving methodologies.

Worksheet Examples & Solutions

PDF worksheets, like those by Kuta Software, provide numerous examples with detailed solutions, enabling students to verify their work and understand problem-solving steps.

Example 1: Solving a Basic Rational Equation

Let’s consider a fundamental example often found in solving rational equations worksheet with answers PDF resources: 9/5 = 4/(x+1). The initial step involves cross-multiplication, yielding 9(x+1) = 4 * 5. Expanding this, we get 9x + 9 = 20.

Subtracting 9 from both sides simplifies the equation to 9x = 11. Finally, dividing both sides by 9 isolates x, resulting in x = 11/9.

Crucially, remember to check for extraneous solutions by substituting x = 11/9 back into the original equation. If the denominator doesn’t equal zero, the solution is valid. Worksheets often emphasize this verification step.

Many PDF worksheets, such as those from Kuta Software, present similar examples with complete solution sets for self-assessment and practice.

Example 2: Equation with a Quadratic Expression

Consider an equation featuring a quadratic expression, commonly found in solving rational equations worksheet with answers PDF materials: 3/x + 1/(x² ‒ 1) = 2. First, factor the denominator: x² ⏤ 1 = (x+1)(x-1). The Least Common Denominator (LCD) is x(x+1)(x-1).

Multiplying both sides by the LCD yields 3x(x+1)(x-1) + x = 2x(x+1)(x-1). Expanding and simplifying results in a quadratic equation. After rearranging, you’ll need to factor or use the quadratic formula to find potential solutions.

Remember to check for extraneous solutions – values that make the original denominators zero (x=0, x=1, x=-1). PDF worksheets often provide detailed steps and solutions for these more complex scenarios.

Example 3: Dealing with Multiple Fractions

Let’s tackle an equation with several fractions, a common challenge in solving rational equations worksheet with answers PDF practice: 1/(x+2) + 2/(x-1) = 3/x. Finding the LCD – x(x+2)(x-1) – is the initial step. Multiplying each term by the LCD clears the fractions.

This results in x(x-1) + 2x(x+2) = 3(x+2)(x-1). Expanding carefully and simplifying the equation is crucial. Combine like terms and rearrange to form a quadratic equation. Factoring or applying the quadratic formula will reveal potential solutions.

Crucially, always verify solutions by substituting them back into the original equation to identify and discard any extraneous solutions. PDF worksheets often showcase this verification process.

Common Mistakes to Avoid

Solving rational equations worksheet with answers PDF practice reveals frequent errors: forgetting extraneous solution checks and incorrectly determining the Least Common Denominator (LCD).

Forgetting to Check for Extraneous Solutions

Extraneous solutions frequently arise when solving rational equations, making verification a critical step often emphasized in solving rational equations worksheet with answers PDF materials.

These solutions appear algebraically correct but don’t satisfy the original equation, typically due to restrictions imposed by the denominators.

Worksheets, like those from Kuta Software, consistently remind students to “check for extraneous solutions” after each problem.

Failing to do so can lead to incorrect answers, as multiplying by the LCD can introduce values that make the original denominators zero, rendering the solution invalid.

Always substitute your solution back into the original equation to confirm its validity; this practice is repeatedly highlighted in educational resources and PDF worksheets.

Remember, a solution must satisfy the original equation to be considered legitimate.

Incorrectly Finding the LCD

A common error when tackling solving rational equations worksheet with answers PDF problems involves miscalculating the Least Common Denominator (LCD). This foundational step is crucial for eliminating fractions and simplifying the equation.

Incorrectly identifying the LCD leads to errors throughout the entire solution process, rendering subsequent steps invalid.

Students often struggle with factoring polynomials within the denominators, hindering their ability to determine the correct LCD.

Resources like Tyler Wallace’s materials emphasize careful factorization before finding the LCD.

Worksheets frequently present equations with varying polynomial complexities, demanding a solid understanding of factorization techniques.

Double-checking the LCD before multiplying both sides of the equation is a vital habit to cultivate, ensuring accuracy and preventing cascading errors.

Resources for Further Practice

Numerous solving rational equations worksheet with answers PDF options are available online, including Kuta Software’s materials, providing ample practice and solutions for skill development.

Online Rational Equation Solvers

Several online tools can assist in verifying solutions obtained from solving rational equations worksheet with answers PDF exercises. These solvers provide step-by-step breakdowns, enhancing understanding beyond simply checking a final answer.

While beneficial, remember these tools are best used after attempting problems independently. Relying solely on solvers hinders the development of crucial algebraic skills.

Many websites offer free rational equation solvers, though accuracy can vary. Cross-referencing results with solutions from reliable PDF worksheets, like those from Kuta Software or resources by Tyler Wallace, is recommended.

These online resources can be particularly helpful when tackling complex equations or verifying solutions found while working through practice problems, solidifying comprehension.

Always prioritize understanding the process over obtaining the answer.

PDF Worksheets with Answer Keys

Numerous solving rational equations worksheet with answers PDF documents are freely available online, offering targeted practice. Kuta Software LLC provides comprehensive worksheets, often including detailed answer keys for immediate self-assessment.

These PDFs typically present a series of equations, progressing in difficulty, allowing students to build confidence and mastery. Tyler Wallace’s resources, licensed under Creative Commons, also offer valuable practice materials.

The inclusion of answer keys is invaluable; students can verify their work, identify errors, and understand the correct solution process. This self-directed learning approach fosters independent problem-solving skills.

When selecting a worksheet, ensure it aligns with your current skill level and learning objectives. Consistent practice with these resources is key to successfully mastering rational equations.

Remember to show your work!

Advanced Topics

Beyond basic worksheets, explore rational inequalities and real-world applications; mastering these builds upon foundational skills practiced with PDF resources.

These extensions demand a deeper understanding of concepts.

Solving Rational Inequalities

Rational inequalities extend the principles of solving equations, requiring a careful analysis of sign changes within the expression. Unlike equations, inequalities often yield solution intervals rather than discrete values.

A crucial step involves identifying critical values – those that make the numerator or denominator equal to zero – and constructing a sign chart to determine where the expression is positive, negative, or zero.

Worksheets focusing on these inequalities, often available as PDF downloads with answer keys, provide targeted practice. These resources typically present inequalities requiring students to find these critical points, test intervals, and express the solution in interval notation.

Remember to always consider restrictions on the variable imposed by the denominator, as these values are excluded from the solution set. Mastering this skill builds upon the foundation established when solving rational equations.

Applications of Rational Equations

Rational equations aren’t merely abstract mathematical exercises; they model real-world scenarios involving rates, work, and proportions. A common application involves calculating the time it takes for two or more individuals to complete a task working together.

Problems often present information as fractions representing work rates, requiring students to set up and solve equations to determine combined completion times. Another application lies in distance-rate-time problems, where rational expressions represent speeds or distances.

Worksheets, frequently found as PDF documents with solutions, present these application problems, demanding translation of word problems into mathematical equations. These resources help students develop problem-solving skills and understand the practical relevance of rational equations.

Successfully tackling these applications reinforces the importance of checking for extraneous solutions within the context of the original problem.